Understanding Angle Relationships - A Geometry Guide

Understanding Angle Relationships - A Geometry Guide

Detail Author:

  • Name : Mr. Deontae Hermiston Jr.
  • Username : estefania75
  • Email : oborer@hackett.com
  • Birthdate : 1973-11-20
  • Address : 603 Rubye Light Apt. 387 South Tyson, ID 20618-8994
  • Phone : +1-678-565-6409
  • Company : Ziemann, Schaefer and Feest
  • Job : Home Entertainment Equipment Installer
  • Bio : Et unde recusandae unde veritatis sed sunt. Quidem et adipisci sapiente nam. Rerum assumenda porro et. Reiciendis quidem aut nihil officia maxime omnis error.

Socials

facebook:

  • url : https://facebook.com/quincy_xx
  • username : quincy_xx
  • bio : Omnis velit laudantium sed qui. Non magni distinctio voluptate similique.
  • followers : 5877
  • following : 981

linkedin:

tiktok:

  • url : https://tiktok.com/@quincy_crona
  • username : quincy_crona
  • bio : Ea non illo suscipit laboriosam et sed. Beatae quas id molestias modi.
  • followers : 5051
  • following : 359

Have you ever stopped to consider how shapes fit together, or what makes one corner look the same as another? It turns out, there's a whole quiet conversation happening between the lines and points that make up our world. Geometry, as a matter of fact, offers us a way to make sense of these connections, especially when we talk about angles. These relationships, you see, are quite important for anyone looking to make sense of the visual information around them.

Angles, which are formed when two lines or rays meet at a common spot, can actually tell us a lot about how things are positioned. They give us a sense of how wide or how narrow an opening is, or how one part of a shape sits next to another. Learning about these connections helps us build a stronger picture of how shapes work, and it's something that, frankly, helps us in many different ways, even if we don't always notice it.

So, we're going to spend a little time exploring these fascinating connections that angles share. We'll look at how they interact, what names we give to these interactions, and how knowing about them can help us figure out missing pieces of a puzzle. This information, you know, is pretty foundational for anyone wanting to get a good grip on how geometry functions, and it's something that, in a way, makes shapes come alive.

Table of Contents

What Are Congruent Angle Relationships?

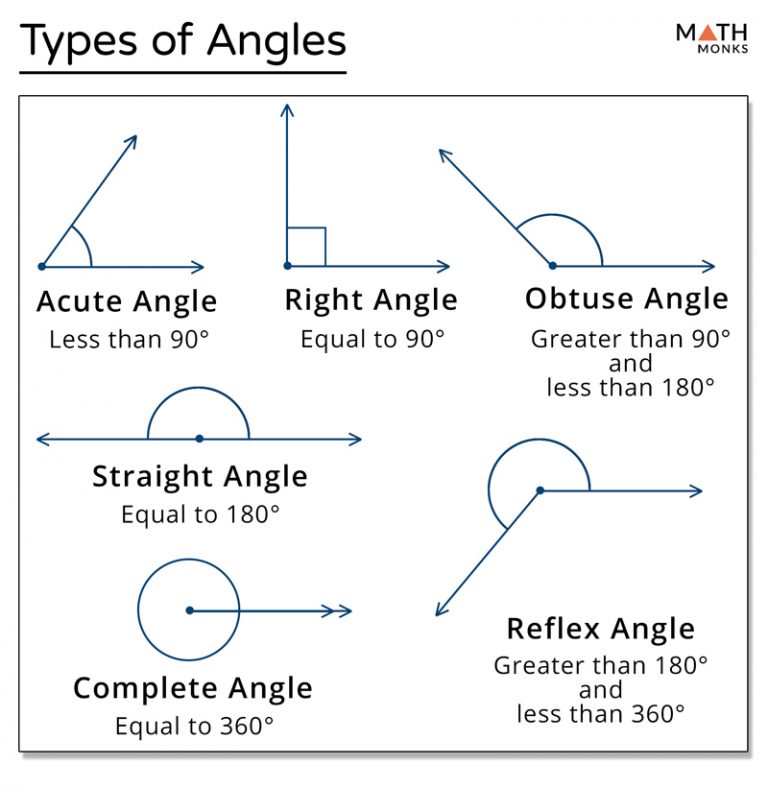
When we talk about angles that are "congruent," what we really mean is that they have the same size, or measure. It doesn't matter how they're turned or where they are located; if their spread, that openness between their two sides, is the same, then they are considered congruent. For example, if you have two corners, and both of them measure exactly 35 degrees, then those two corners are, in fact, congruent. They show the same amount of openness, even if one is pointing up and the other is pointing down, or if they are made with different kinds of lines, so that's pretty neat.

This idea of sameness in angle relationships is pretty basic, but it's something we use a lot. You might see two triangles that look different, but if certain angles inside them have the same measure, it tells you something important about their overall shape. It's almost like saying two people have the same height, even if one is standing and the other is sitting down. The core measurement, you know, remains the same. This concept, of course, helps us compare and contrast different geometric figures and understand their properties more completely.

So, when you see a problem asking about congruent angles, just remember it's about whether they have an equal measure. It's a simple idea, but it's a very powerful one in geometry. It allows us to say, with certainty, that two different angles are, in a way, identical in their fundamental characteristic, which is their size. This is just a starting point for understanding how angles connect, but it's a pretty important one to get a handle on, to be honest.

How Do We Describe Angles That Sit Next to Each Other? (Adjacent Angle Relationships)

Imagine two angles that are practically neighbors. They share a common side and a common point where they meet, but they don't overlap. These are what we call "adjacent" angles. Think of it like two rooms in a house that share a wall. They're right next to each other, and they touch, but they're still separate rooms. This kind of angle relationship is, in some respects, pretty straightforward to spot once you know what to look for, and it comes up quite a bit in different shapes.

For instance, if you look at a corner of a square, and then you draw a line from that corner out into the square, you've just created two adjacent angles. They both use that new line as one of their sides, and they both meet at the square's corner. They're right there, side by side, basically sharing a boundary. This setup is very common in geometric drawings, and it's a good first step to seeing how angles can be related by their physical placement, you know, next to each other.

Recognizing adjacent angle relationships helps us break down more complex figures into simpler parts. It's like taking a big problem and looking at its smaller pieces. Knowing that two angles are adjacent doesn't necessarily tell you their measures, but it does tell you how they are positioned relative to each other, which can be pretty useful. It's a fundamental way angles can interact, so it's a good one to keep in mind, too it's almost a building block for other relationships.

What Happens When Angles Add Up to Special Numbers? (Complementary and Supplementary Angle Relationships)

Sometimes, angles team up to make a specific total. When two angles, when put together, measure exactly 90 degrees, we call them "complementary." Think of a perfect corner, like the corner of a book or a table. If you can split that corner into two smaller angles, and those two smaller angles combine to form that perfect 90-degree corner, then they are complementary. This is a very common angle relationship, and it's something you'll see a lot in geometry, especially with right angles.

Then there are angles that are "supplementary." These are two angles that, when added together, make a straight line, meaning they total 180 degrees. Imagine a perfectly flat surface, like a tabletop. If you draw a line across it, and then another line comes off that first line, the two angles formed on one side of the second line will be supplementary. They basically complete a half-turn. This angle relationship is, honestly, just as important as complementary angles, and they both help us find missing angle measurements pretty often.

Understanding complementary and supplementary angle relationships is pretty key because they give us a way to figure out an unknown angle if we know its partner. If you know one angle in a complementary pair is 30 degrees, you can easily figure out the other must be 60 degrees. Similarly, if one angle in a supplementary pair is 70 degrees, its partner must be 110 degrees. This is, in a way, a very practical application of how angles connect and how their measures relate to each other, so it's definitely something to get comfortable with.

Can Angles Be Opposite Each Other? (Vertical Angle Relationships)

Picture two straight lines crossing each other, like an 'X' on a piece of paper. When lines cross, they create four angles. The angles that are directly across from each other, sharing only a common point where the lines intersect, are called "vertical angles." What's really cool about vertical angle relationships is that these angles are always, without exception, congruent. If one angle measures 50 degrees, the angle directly opposite it will also measure 50 degrees. This is, you know, a pretty powerful rule in geometry.

This property of vertical angles is incredibly useful for solving problems where you need to find unknown angle measures. If you're given the measure of just one angle formed by two intersecting lines, you can instantly know the measure of the angle opposite it. It's almost like a built-in shortcut. This relationship helps simplify many geometric puzzles and is, in fact, a cornerstone for more complex proofs and calculations down the line. It's a rather elegant concept, when you think about it.

So, whenever you see two lines crossing, remember to look for those pairs of angles that are directly opposite. They're guaranteed to be the same size. This makes figuring out missing pieces of information a lot easier. It's a simple observation, yet it carries a lot of weight in how we understand the connections between angles formed by intersecting lines. It's just a really handy thing to know, actually, and it comes up all the time.

Linear Pair Angle Relationships

Let's go back to those two lines crossing, but this time, let's look at the angles that sit next to each other on a straight line. When two adjacent angles combine to form a straight line, they are called a "linear pair." And here's the kicker: the angles in a linear pair are always supplementary, meaning their measures add up to 180 degrees. This is, basically, another very common angle relationship you'll encounter, and it's closely tied to the idea of a straight angle.

Imagine a straight road, and then another road branches off it. The angle formed by the straight road and the branching road, plus the angle formed by the branching road and the rest of the straight road, will form a linear pair. They share a side, meet at a point, and together they make a perfect half-circle, or 180 degrees. This relationship is, quite frankly, super helpful for finding unknown angles, especially when you have lines intersecting, and you know one of the angles involved.

So, if you spot two angles that are side-by-side and together they make a straight line, you can be sure their total measure is 180 degrees. This is a pretty dependable rule. It's like having a known total, and if you know one part, you can easily figure out the other. This type of angle relationship is, in a way, a practical application of supplementary angles, but specifically for angles that share a common side and form a straight line, so it's a bit more specific.

Parallel Lines and Angle Relationships: Corresponding and Alternate Angles

Things get even more interesting when we introduce parallel lines. Parallel lines are lines that run side-by-side and never meet, like railroad tracks. When a third line, called a "transversal," cuts across two parallel lines, it creates a whole bunch of angles, and these angles have some really special relationships. For example, "corresponding angles" are angles that are in the same relative position at each intersection. They're like matching corners if you were to slide one intersection onto the other. And here's the cool part: corresponding angles are always congruent when the lines are parallel. This is, you know, a very important concept in geometry.

Then there are "alternate interior angles." These are angles that are on opposite sides of the transversal and between the two parallel lines. They're inside the "tracks," but on different sides of the crossing line. Just like corresponding angles, alternate interior angles are also congruent when the lines are parallel. So, if one alternate interior angle measures 60 degrees, the other one will also be 60 degrees. This relationship, too it's almost like a hidden pattern, helps us prove lines are parallel or find missing angle measures, which is pretty neat.

We also have "alternate exterior angles," which are on opposite sides of the transversal but outside the parallel lines. And guess what? They're congruent too! These angle relationships—corresponding, alternate interior, and alternate exterior—are, in fact, incredibly powerful tools for working with parallel lines. They allow us to make deductions about angle measures just by knowing that lines are parallel, or conversely, to prove that lines are parallel if we know these angle pairs are congruent. It's a pretty fundamental set of ideas, honestly, for understanding how lines and angles interact on a larger scale.

Using Equations to Find Unknown Angle Relationships

One of the most practical things about learning these angle relationships is that they give us a way to figure out angles we don't know. Often, in geometry problems, you'll be given a picture with some angles labeled with numbers and others labeled with letters, like 'x' or 'y'. The relationships we've talked about—like complementary angles adding to 90 degrees, or a linear pair adding to 180 degrees, or vertical angles being equal—allow us to set up simple equations. This is, in a way, where the real problem-solving comes in, and it's quite satisfying to see it work.

For example, if you have two angles that form a linear pair, and one of them is labeled 120 degrees, and the other is labeled 'x', you know that 120 + x must equal 180. From there, it's just a simple bit of algebra to solve for 'x'. Similarly, if you have two vertical angles, and one is 75 degrees and the other is 'y', you immediately know that 'y' must be 75 degrees because vertical angles are always the same. This ability to translate visual information into mathematical statements is, you know, a pretty big step in understanding geometry more deeply.

Practicing these types of problems helps build a stronger grasp of how angles behave. It's not just about memorizing names; it's about seeing how these connections play out in real figures and using them to find answers. So, when you see a problem with an unknown angle, remember the relationships we've discussed. They are, in fact, your key to setting up the right equation and solving for that missing piece. It's pretty much like solving a little puzzle every time, which can be quite fun, actually.

Practical Uses for Angle Relationships

You might wonder, "Why do I need to know all this about angle relationships?" Well, it turns out these concepts are not just for textbooks; they show up in the real world more than you might think. From building houses to designing bridges, engineers and architects use angle relationships constantly to make sure structures are stable and safe. Think about the angles in a roof truss, or the way a bridge cable connects to its support tower. Every single angle has to be just right, and knowing these relationships helps professionals calculate them with precision. This is, in fact, a very practical application of what we've been discussing.

Beyond construction, angle relationships are also really important in fields like surveying, where people measure land and create maps. Surveyors use specialized tools to measure angles between points to accurately plot out property lines or terrain features. Similarly, in fields like computer graphics and animation, understanding how angles work is essential for creating realistic movements and three-dimensional objects. If a character's arm bends, the software needs to know the angle relationships to make it look natural. It's pretty fascinating, when you think about it, how these basic geometric ideas underpin so many different areas.

Even in everyday life, without realizing it, we use a basic sense of angle relationships. When you park your car, you're judging angles. When you set up furniture, you're considering how pieces fit together at certain angles. While you might not be writing equations, the fundamental ideas are still there. So, these angle relationships are, in some respects, more than just abstract ideas; they are tools that help us interact with and shape the physical world around us. They are, quite simply, a part of how things work, and knowing about them gives you a bit more insight into that, too it's almost like having a secret language for shapes.

Angle – Definition and Types with Examples

Angle – Definition and Types with Examples

Angles - Meaning | Definition | Examples | What are Angles?

Related Post

Ariel Rebel - Life, Work, And Online Presence

Miranda Lambert - Bring Me Down

Maura Murray Father - A Name's Deep Meaning

Nobody Wanna See Us Together But It Don't Matter No - A Look At Hidden Strength